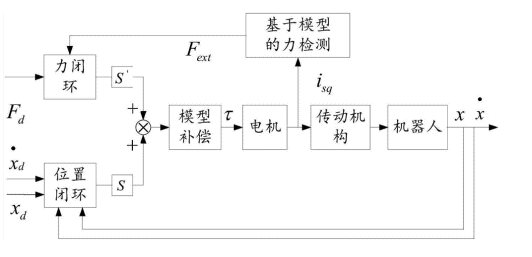
如果想快速入门四足机器人步态控制算法,我们还提供了自研的开源站立步态例子,其运行了完整的状态估计、MPC控制、运动学逆解位力混合控制,通过该例子可以了解基本的力控制框架,对于后续学习MIT或更复杂的项目提供了便利。
我们开源了采用MPC的基本站立控制程序,其首先基于卡尔曼滤波器完成对机器人状态的估计,通过遥控器完成期望指令的给定,采用MPC完成力控制,然后通过运动学逆解的位力混合控制实现高效的控制,代码移植了除WBC外的大部分核心内容,相关控制原理可以参考MIT论文和资料,下面介绍一下主要的简化部分,本开源项目下载地址:
软件功能介绍
首先介绍下站立Demo的基本使用方法,在启动程序前首先运行默认的hardware和navigation程序,确保上位机和遥控器连入,长期X和RR完成初始化腿部复位,按LL完成站立,此时右摇杆对应姿态调节,扳机键对应航向调节,左摇杆对应质心位置调节,RR下蹲,Y软模式保护,下急停保护。
相比MIT原始代码我们提供的开源教学版本程序主要采用了运动学逆解的方式来替代WBC规划产生期望足端位置并进一步转化为关节角度,同时采用单腿动力学补偿电机重力项,由于代码较为繁琐建议用户自行进行学习和阅读并与我们官方群内进行沟通一起完善相关教程,下面仅给出简单的代码逻辑流程。
在locomotion_sfm中为系统状态机调度,基于遥控器完成对步态的初始化和更新:

Odom_kf中为移植MIT的卡尔曼滤波器:
各关节角度和运动学解算值作为输出,输出vmc_all的机体状态,进一步在MPC代码中建立了独立的线程用于预测模型的求解,此部分与MIT的类似,只不过将摆动轨迹规划剥离出来降低对CPU计算资源的占用率。
最终,将MPC计算的足端力转换扭矩指令,为保证高精度的力跟踪,引入基于运动学逆解的位置规划,最终将二者合并的扭矩指令下达实现位力混合控制:
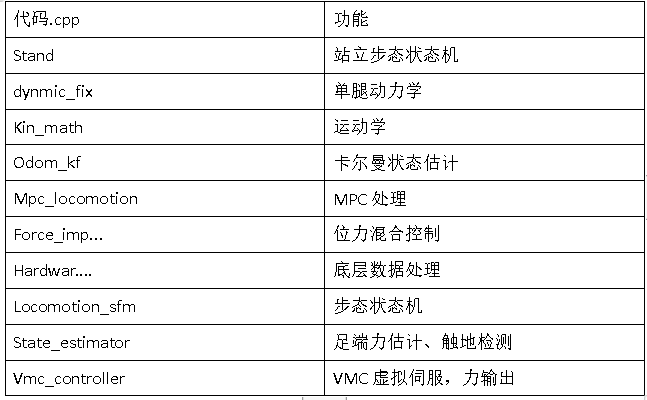
则下表中给出了各代码部分的主要介绍:
基本控制原理介绍
本例程中搭建完整的MPC力控制与KF状态估计框架,其移植与MIT相关源码,对于力控制可以参考相关论文与资料,目前网络上已经有很多丰富的资料,这里提供一个合集地址:
对于四足机器人基本运动控制来说,目前主要采用的方法是将四足机器人简化为单刚体质点模型,各腿虚拟腿点支撑模型,通过构建这样一个多点支撑的控制问题,来解决四足机器人的质心状态的控制问题,即在一定程度上对系统模型进行了解耦,而落足点控制则基于最经典的Raibert倒立摆模型即可。因此对于目前的控制方法来说机器人支撑状态的力控制是最重要的,也是目前很多论文研究的核心问题,对于摆动控制来说由于倒立摆模型很简单因此更重要的是为其提供一个准确、高动态的状态估计,从而快速克服外力扰动,基本的多点支撑单刚体模型与动力学如下:
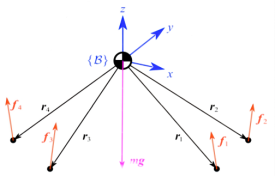
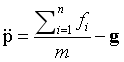
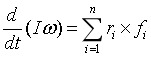
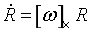
针对上述模型其最大的特点一是欠驱动即支撑腿只能产生正向力,另外是非线性与无人机类似由于系统模型包含旋转姿态的正余弦值,完整的模型仍然是非线性的,另外上面仅考虑了全支撑状态,如需要考虑具有腾空相步态的控制其还是一个控制输出受约束的系统模型。本例子仅介绍了腿支撑的站立步态基本控制方法。
1)4腿支撑力控制
4腿支撑控模型即标准的MPC控制模型,在站立时首先完成4条腿运动学解算,为了简化问题,我们在程序在控制中没有考虑当前机器人的朝向角,即在MPC控制模型中仅包含了俯仰和横滚的变化,支撑点位置也没有考虑航向的变化,旋转存在的误差仅通过提高控制频率来实现,另外为了保证转向机动稳定,我们在KF中还是保留了考虑航向的模型,最终采用转换到机体的速度积分得到不需要航向控制的MPC程序中。相关具体内容可以查看我们的开源代码;
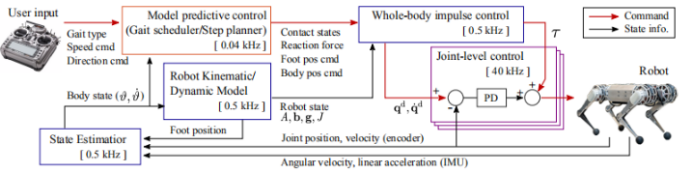
2)基于运动学逆解的位力混合控制
基于MPC可以完成足端力的求解,从而时间机器人的系统状态的闭环,但是在实物系统中由于模型的误差或伺服驱动带宽限制,使得力控制参数难以整定,其中最大的原因就是实物样机接触状态难以估计,导致足端支撑出现间隙,力随之剧烈抖动。
因此以MIT猎豹为例其后期版本增加了WBC全身动力学控制,即在力控制基础上增加了位置环的规划,实现位力混合控制,在保证力控高带宽、高响应、高抗扰的同时,通过位置环控制抑制末端的抖动或滑移,那其中最重要的问题就是如何规划得到当前的位置与关节角度。
我们在开源代码中没有采用WBC算法,而基于运动学逆解构建了一个基本的位力混合控制框架。核心原理是机器人处于4腿支撑,由于已经知道期望的质心状态,则可以通过求解4腿运动学与机体的相对变化关系得到各足端在机体坐标系下的位置,进一步通过运动学逆解求取关节角度即可。
- 相关资料:
https://zhuanlan.zhihu.com/p/64321561
https://blog.csdn.net/weixin_45417246/article/details/115862456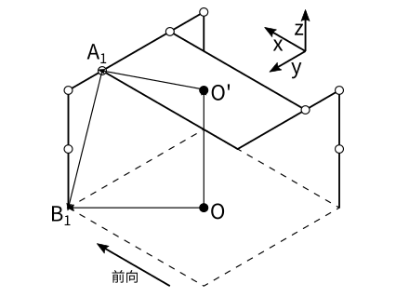
如上图所示给出了基本的示意图,通过期望值我们可以构建机体质心,相对地面的变换坐标系:
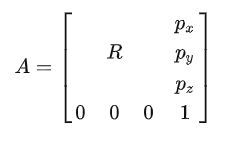
由于我们在进入站立模式后期望足端位置不再发生变化,因此可以得到每个腿在世界坐标系下的固定位置B,则我们的目的就时求取各腿足端B相对髋关节A点向量,从而也就得到了足端在髋关节坐标系下的位置:
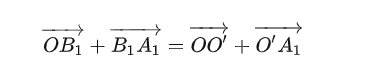
通过等式调节最终得到:
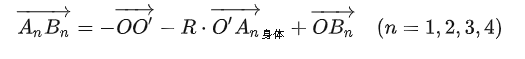
最终将足端位置带入运行学逆解既可以求取到关节角度,构建PD控制器完成闭环,将扭矩与MPC足端力由雅克比转换得到的扭矩相加共同输入到电机指令中。
注:这里提一句,由于Tinymal采用节点盒完成关节PD控制,因此只下发了扭矩前馈,节点盒完成位置扭矩的融合。